函式y=(x^2+4)√(x^2+1)的主要性質
主要內容:
本文介紹函式y=(x^2+4)√(x^2+1)的定義域、單調性、凸凹性、奇偶性及極限等性質,並透過導數知識計算函式的單調和凸凹區間。
※.函式的定義域
函式y=(x^2+4)√(x^2+1)為二次函式的乘積,根據函式的特徵,函式自變數x可以取全體實數,即函式的定義域為:(-∞,+∞).
※.函式的單調性
∵ y=(x^2+4)√(x^2+1)
∴ y'=2x√(x^2+1)+(x^2+4)*x/√(x^2+1)
=[2x(x^2+1)+(x^2+4)*x]/√(x^2+1)
=3x(x^2+2)/√(x^2+1)
令 y'=0,則x=0 。即:
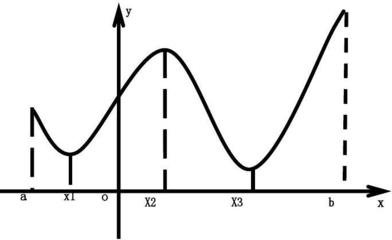
(1).當x∈(-∞,0)時, y'<0,此時函式y為減函式,區間為減區間。
(2).當x∈[0,+∞)時, y'≥0,此時函式y為增函式,區間為增區間。
※.函式的凸凹性
∵y'=3x(x^2+2)/√(x^2+1)
=3(x^3+2x)/√(x^2+1)
∴y〞=3[(3x^2+2)√(x^2+1)-(x^3+2x)x/√(x^2+1)]/(x^2+1),
=3[(3x^2+2)(x^2+1)-(x^3+2x)x]/√(x^2+1)^2,
=3(2x^4+3x^2+2)/√(x^2+1)^2>0,
則函式在定義區間上為凹函式。
※.函式的極限與極值
lim(x→-∞)(x^2+4)√(x^2+1)=+∞,
lim(x→+∞)(x^2+4)√(x^2+1)=+∞,
lim(x→0)(x^2+4)√(x^2+1)=ymin.
※.函式的奇偶性
∵f(x)=(x^2+4)√(x^2+1)
∴f(-x)=[(-x)^2+4]√[(-x)^2+1]
=(x^2+4)√(x^2+1),
即f(-x)=f(x),則函式在定義域上為偶函式,
函式y=(x^2+4)√(x^2+1)影象關於y軸對稱。