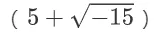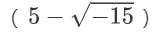撰文 | 顧雪梅 林梅
量子力學建立之初,薛定諤將虛數i引入方程,用來描述微觀粒子的奇特行為。但是,複數究竟是一種數學技巧,還是客觀實在,一直沒有答案。如果我們不用複數,而只用實數來描述量子世界,是可行的嗎?複數在量子力學裡,是非用不可的嗎?
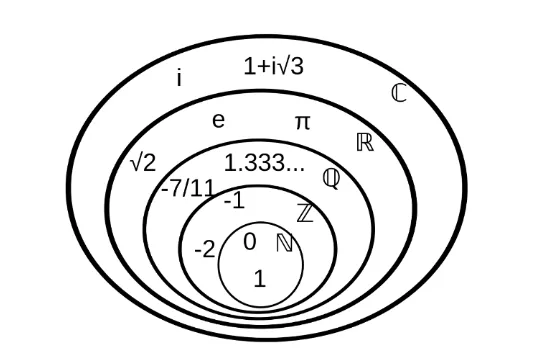
數學,幾乎伴隨著我們每個人的認知。在我們很小的時候,家長很可能會用一個個蘋果、一根根手指,來教會我們計數;後來,數字的範圍不斷擴充套件,當初通過幾個蘋果、幾根手指建立起來的對數字的理解,已經不能涵蓋人們遇到的所有場景了。
幾千年前,出於生產生活的需要,我們不僅需要表示“盈餘”,還要表示“虧空”,所以,人類跨域了正數和零的概念,負數產生了;同樣是在幾千年前,當我們需要描述把單位“1”分成若干份的時候,分數就產生了。分數可以化作有限小數或無限迴圈小數。還有一些數“不講道理”,它化作的小數既不終止,也不重複,而是無限不迴圈的,我們管它叫無理數。我們比較熟悉的無理數有圓周率、還有邊長為1的正方形對角線長度根號2 。可以看到,哪怕是最“不講道理”的無理數,在圓形、正方形這樣的日常生活場景中也能找到它們的身影。只要你承認圓形、正方形存在,就得承認無理數的存在。
圖片來自維基百科
數字的應用在生活中太重要了,世界上各個文明哪怕相隔萬里,都不約而同地在數字上產生過燦爛的文化和悠久的歷史。
但無論如何,上面提到的這幾類數字不管多抽象,總還可以在現實中找到對應的意義。直到,你遇到了——複數。
複數由實部和虛部組成,其中虛部那個令人困惑的 i ,儘管你知道它代表了-1的平方根,但是它究竟有什麼意義、對應現實世界的什麼場景,可能大部分人都說不上來。
這個問題,連偉大的數學家也感到過困惑。
16世紀,義大利數學家吉羅拉莫·卡爾達諾曾經在他的一本名叫《大術》的著作中,為了討論“把10分成兩部分,使它們的乘積為40”的問題,引入了將負數取平方根的方法,他把兩個數分別寫成
和
,解決了這個問題。當時,他也只是認為這是一種方便計算的數學技巧,還沒有意識到自己觸控到了複數宮殿的大門。
後來,笛卡爾將負數取平方根的表達命名為虛數。這個虛數,好像一個似有若無的幽靈,當時的數學家難以洞悉它的秘密,經過200多年很多數學家們的前赴後繼,複數理論才建立起來。它的重要性令人驚歎,難怪法國數學家阿達馬說:“在實數域中,連線兩個真理的最短路徑是透過複數域。”
複數理論在數學界的地位日漸上升,在物理學和其他工程技術上也都是十分重要的工具。我們計算電流、處理訊號,都離不開復數這個工具。但是,也僅僅是工具而已。什麼意思呢?就是,有了它我們可以更方便地處理問題,沒有它,也可以搞定,只不過麻煩一些。畢竟,最終我們計算出來的電流總應該是個實數。
但是,有一天,這種確定性到量子力學這兒開始動搖了。像16世紀的數學家一樣,對於虛數的困惑也浮現在物理學家心裡。
1926年,物理學家薛定諤在建立波動方程的時候,最初參照波動光學的模型,寫下了機械粒子的微分方程,但這個方程沒有任何物理上的意義,然而當他將負1的平方根 i 放入到方程裡時,複數形式的波函式瞬間變得有意義了,能夠幫助我們準確描述粒子的量子行為。而波函式這種看不見摸不著的抽象概念,不管是薛定諤本人,還是其他物理學家,誰都說不清它的本質到底是什麼。
但對於我們而言,物理研究的是現實世界,而現實世界你能想象到的一切物理量應該是可測量的,而可測量的量裡面怎麼會有虛數呢?
我們知道,波函式的模方描述的是粒子出現的機率,所以,雖然波函式寫成複數形式,但是機率本身還是實數。那麼,虛數 i 真的是描述真實世界所必需的嗎?薛定諤也不確定。在他給洛倫茲的信中,他似乎傾向於虛數 i 只是一種數學上的處理方法,而現實中的可測物理量都應該是實數形式的。當時,他在信中就表示過,波函式引入複數,自己是不太踏實的,本質上量子波函式應該是一個實函式。薛定諤一直試圖把複數從他的波動方程中抹去,但是並沒有成功。
在量子力學中,複數是必要的嗎(圖片來自Quanta Magazine)
那麼,複數的波函式和真實的量子世界是什麼關係?複數到底在裡面扮演何種角色呢?
要回答這個問題,我們可以回頭看看無理數的誕生。兩千多年前,無理數的誕生是為了描述邊長為1的正方形的對角線長度,只要你承認正方形的存在,就得承認無理數是客觀存在的,否則,對角線長度用什麼來表示呢?可見,無理數並非是“沒道理的”。那麼虛(復)數呢,它真的是虛的嗎,還是具有客觀實在性?
現在的複數之於量子世界與當初的無理數是類似的道理。
一般而言,每一個波函式對應著一種物理狀態的分佈。此外,我們認為獨立構建的體系具有獨立的物理狀態,那麼很自然地,由這些獨立系統構成的總的物理狀態可以直接用它們的張量積形式來表示,這有點類似於在數學裡我們把兩個或者以上的數進行相乘來得到一個總的結果。
當兩個波函式分別由完全相同、互相獨立的兩個系統製備時,研究證明它們對應的分佈沒有重疊,也就是說一個物理狀態只能夠被編碼到唯一的波函式當中,這也就意味著波函式是客觀真實存在的[1]。而如果我們可以證明,量子力學(波函式)必須使用複數,那麼複數就是客觀實在的。
所以,現在的問題歸結到了:量子力學真的必須使用複數嗎?換句話說,如果不用複數,除了過程麻煩點兒,計算結果會不同嗎?
在經典世界裡,我們知道複數一般可以寫成
,那麼理論上,我們總可以用a和b這兩個實數來替代,只不過,一個複數變成兩個實數,處理起來麻煩一些。而對於量子世界,很多科學家也在不斷嘗試用各種不引入複數的方法來描述量子力學。
我們知道,量子力學具有獨特的數學結構,其中不同的物理系統狀態用不同的希爾伯特空間來描述,位置或者動量等可觀測量則用作用於系統的希爾伯特空間的線性運算元表示。從量子力學的早期開始,科學家們就認為複數框架下的量子理論的許多特徵被兩個替代的假設理論所表示,比如複數的希爾伯特空間可以被一個實數或四元數的希爾伯特空間所取代。這在1936年伯克霍夫和馮·諾依曼提出量子邏輯假設時就被明確指出,量子態的希爾伯特空間的閉子空間可以構造一種類似布林邏輯的代數語義,基於此,實數和四元數的模型與標準的複數理論一樣可以滿足他們的假設。
另一方面,在1960年,瑞士物理學家厄恩斯特·斯蒂克爾堡為了將標準復量子理論實數化,引入了特殊的運算元,並要求可觀測的量與引入的運算元對易,這類似於數學中的交換律。由於對可觀測量的這種限制,他的特殊運算元扮演著虛數 i 的角色,規則雖然麻煩點,但最終結果在實數框架下沒有任何影響。雖然當時他只是證明了所有單粒子實驗的量子理論預測都可以在只用實數的情況下推匯出來,但他的這種規則可以進一步擴充套件應用到多粒子體系。
還有一些研究表示,在量子世界裡,在不使用複數的情況下,透過引入可以與系統中的任何東西進行相互作用的通用量子位元,把狀態和測量空間維度擴大一倍,就像經典物理裡,用a和b兩個數代替一個複數一樣,我們依然可以完美預測著名的量子物理實驗——貝爾實驗。(貝爾實驗是一個檢驗量子力學基礎理論的重要實驗,它探究的是關於糾纏的根本性質。它將糾纏粒子分別傳送給Alice和Bob,就像分別、同時、背靠背地拷問一對雙胞胎一系列問題,根據它們的回答,來看看雙胞胎之間的心有靈犀,究竟是真的跨越時空的糾纏,還是有誰偷偷傳遞了訊息。)
除了薛定諤、斯蒂克爾堡,還有馮諾依曼、戴森(Freeman Dyson)(對,就是寫《飛鳥和青蛙》的那個)、奇森(Nicolas Gisin)、伍特斯(William Wootters)也做了很多實數量子力學的嘗試。這些研究讓物理學家一度認為複數在量子力學裡只是為了我們方便計算的手段,而不是必需的存在,似乎我們完全可以只用實數去描述我們的世界。
猜測歸猜測,物理規律的證明始終是需要實驗資料來支撐。2021年1月,一個嶄新的方案由西班牙、奧地利和瑞士等國科學家組成的理論團體提出來。這個方案的獨特之處在於,它是實驗可檢驗的、定量的、類似於貝爾不等式的判據。
圖片來自APS Physics
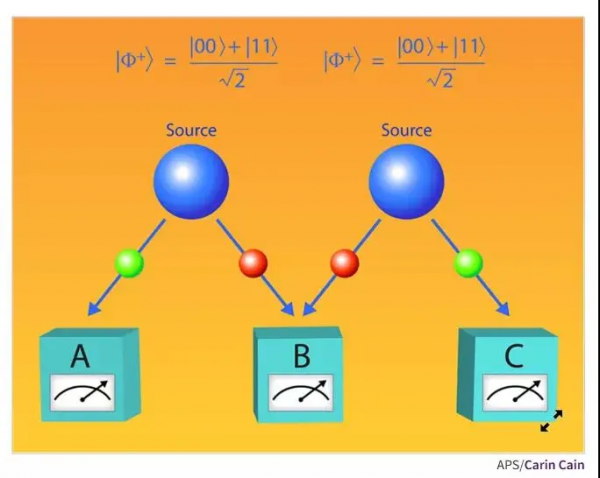
所謂糾纏交換,就是說,Alice、Bob、Clarie三個人不在一處,這時,兩個糾纏源R和S,S將一對糾纏粒子傳送給Alice和Bob;R將另一對糾纏粒子傳送給Bob和Clarie,根據Bob進行的貝爾測量結果,Alice和Clarie手中原本沒有關聯的粒子最終處於糾纏狀態。早期的貝爾測試中,所有參與方的粒子來自單一的源,他們額外攜帶的資訊在實數描述中不是問題。
但是在新設計的貝爾測試中,兩個糾纏源相互獨立,參與三方各自獨立地進行本地的測量。當Bob做完整的貝爾測量、Alice和Clarie執行各自的測量時,三方關聯的統計結果如何?科學家們的理論計算表明,如果我們採取沒有虛數的所謂“實量子理論”,並且我們認同獨立子系統是以張量積的形式構成整個系統,那麼得到的預測結果將與複數模型下的預測不一致。這樣複數描述量子力學是否必要,就成為了一件可以驗證的事。
該理論成果最初1月提交到了科學預印本伺服器arXiv上,於2021年12月正式發表在了《自然》雜誌上[2]。
圖片來自nature
遊戲規則既然有了,接下來,只需要設計一些好的實驗裝置來完成這種驗證。它必須滿足很多嚴苛的條件,比如:需要實現確定性的糾纏交換(需要確定性的CNOT門),如果是用光子做糾纏粒子的話,要能對光子的偏振進行有效的測量,Alice、Bob、Clarie三人要保證類空間隔以防止“相互串供”,等等。
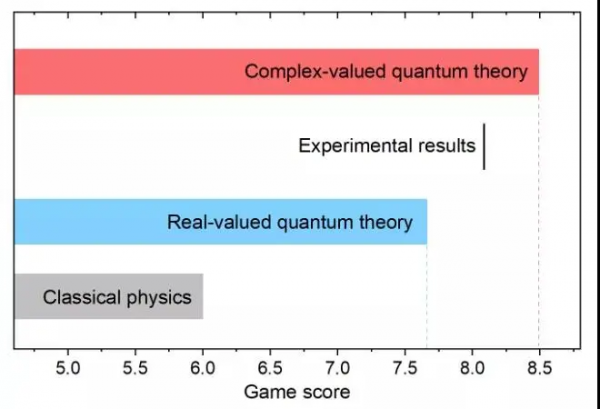
2021年3月,中國科學技術大學潘建偉、陸朝陽、朱曉波等組成的研究團隊基於自主研發的超導量子體系,首次對量子力學中複數的必要性進行了實驗檢驗[3]。他們採用了I形的Transmon量子位元設計來增加量子位元之間的間距,以減少在同一個超導晶片上的位元之間的近鄰耦合。透過高精度的量子操控技術,兩個糾纏脈衝序列用於製備兩對糾纏態,將量子位元分發給參與的三方。每一方各自獨立選擇要在其量子位上執行的測量操作,其中Bob進行完整的貝爾態測量。最後,根據測量結果的聯合統計分佈計算量子博弈遊戲的"分數",僅用實數的參與者最多可以獲得7.66分,而實驗結果顯示,由4個超導量子位元組成的三方參與者可以獲得8.09(1) 分,以超過判據43個標準差的實驗精度證明了複數在標準量子力學形式中的必要性。這個實驗的優勢是確定性的糾纏交換和量子位元測量,關閉了探測效率潛在的漏洞。
實驗結果圖:不同的理論對應不同的數值界限,實驗測量結果大大超過了實數量子力學模型(圖片來自陳明城、王粲、劉豐銘等PRL 128, 040403 (2022))。
2021年10月,南方科學技術大學的範靖雲研究團隊以同樣的概念為基礎,在光學體系上進行了複數檢驗實驗[4]。實驗中,同一個實驗臺上的兩個獨立源產生糾纏的偏振光子對,分發給遊戲的三方。Alice和Clarie利用本地的波片組合對各自接收到的光子進行相應的隨機測量操作。這個實驗的原型來自1998年潘建偉和同事在因斯布魯克利用線性光學完成的首個糾纏交換的實驗[5]。南科大研究團隊透過修改複數和實數的博弈遊戲協議,使Bob可以利用線性光學器件進行機率性的貝爾態測量來完成驗證。最終,參與三方根據聯合測量結果以超過判據4.5個標準差的實驗精度得出了相同的結論,也就是量子物理需要複數。
兩項獨立研究成果於2022年1月24日同時發表在國際知名學術期刊《物理學評論快報》上,確立了量子力學需要複數。但是,在這兩個實驗研究中,所有的量子態製備和遊戲三方的本地測量並沒有遵守理論設計要求的嚴格類空分離,使得在複數和實數博弈的遊戲中,理論上,實數參與者可以作弊,利用潛在的漏洞獲得和複數參與者相同的分數,從而導致實驗不能區分實數和複數描述框架下的量子力學。
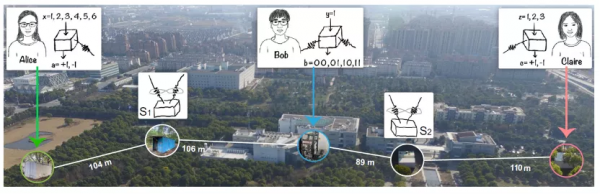
基於此,中國科學技術大學潘建偉、陸朝陽、張強等進一步開展了基於光子體系下嚴格滿足愛因斯坦定域性的實驗檢驗[6]。在這個實驗中,研究人員利用光量子網路中的兩個獨立源各自獨立產生糾纏光子對,分發給遠處的三個參與者進行高速隨機的光子測量操作。遊戲過程中,參與者不受其他參與者的測量選擇和結果影響,獨立地進行各自本地的操作。實驗結果顯示,實數描述下的參與者與光學量子網路實驗中觀察到的資料不相容,近一步支援證明了複數是描述量子物理必不可少的存在。
非定域實驗裝置圖。實驗三方處於類空間隔,滿足嚴格的愛因斯坦非定域性條件。(來自吳典、江揚帆、顧雪梅等arxiv.2201.04177, PRL to appear)。
現在,透過實驗已經驗證了,虛數 i 不只是一個工具,而是一個必不可少的存在。在“獨立系統以張量積形式構成總的物理狀態”這種自然的假設下,證明了量子力學的波函式是客觀實在的,並且量子力學中複數是必需的,那麼這也就意味著複數具有客觀實在性,不再僅僅是個數學技巧而已。這就好比我們前面說的,只要你承認正方形的存在,承認有正方形對角線長度,就得承認無理數的客觀實在性。當然,至於是不是接受張量積假設,正如是否接受世界上存在正方形一樣,你可以保有自己的看法。
回到基礎物理的角度,筆者想到楊振寧先生曾經在臺中央大學的一次演講中,也曾提到過 i 在量子力學發展之後的重要作用。他認為,i 應該不只是一個工具,更是一個基本觀念。但為什麼基礎理論必須引入 i ,卻沒有人知道。
,時長01:09
楊先生提出的第二個問題——為什麼會如此,還會吸引著物理學家們繼續追問下去。有可能,現在的我們就像當年寫出
的吉羅拉莫·卡爾達諾一樣,觸控到一個新世界的大門,它正等著人類去推開。
製版編輯|-小圭月-
參考文獻:
[1]https://www.nature.com/articles/nphys2309
[2]https://www.nature.com/articles/s41586-021-04160-4
[3]https://journals.aps.org/prl/abstract/10.1103/PhysRevLett.128.040403
[4]https://journals.aps.org/prl/abstract/10.1103/PhysRevLett.128.040402
[5]https://journals.aps.org/prl/abstract/10.1103/PhysRevL